Precedente capitolo:
c-e-molta-strada-da-fare-7.html
Prosegue in:
Aggiornamento sugli esperimenti dei neutrini ore 20,00
del 23/02/2012:
ereditato-opera-neutrini-19415.html
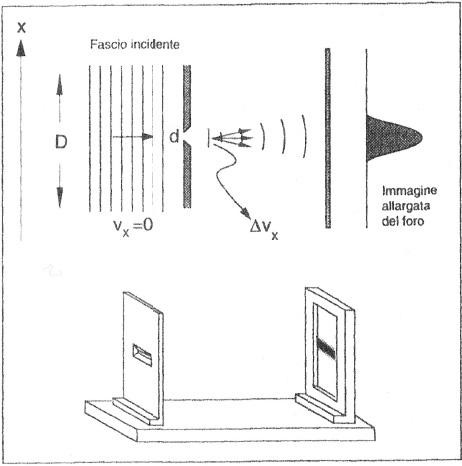
Per risolvere questo paradosso, vi ricorderò un principio
fondamentale: per calcolare correttamente la probabilità
di un evento si deve ‘definire con chiarezza l’evento com-
pleto’, in particolare quali siano le condizioni iniziali e fi-
nali dell’apparato.
Si devono controllare gli strumenti di misura prima e do-
po l’esperimento e cercare le eventuali variazioni.
Quando prima calcolavamo la probabilità che un fotone
da S a D senza rivelatori in A e in B, il fenomeno consiste-
va semplicemente nello scatto del rivelatore in D.
Quando tale scatto era l’unico cambiamento nell’apparato
di misura, non c’era modo di conoscere il percorso scelto
dal fotone e si osservava interferenza.
Mettendo rivelatori in A e in B, abbiamo cambiato il proble-
ma.
Adesso ci sono ‘due’ eventi completi, cioè due insieme di
condizioni finali, distinguibili:
1) scattano i rivelatori in A e in D;
2) scattano i rivelatori in B e in D.
Essendovi diverse condizioni finali possibili, si deve calcola-
re la probabilità di ciascuna di esse come evento separato e
completo.
Per calcolare la probabilità che vi sia uno scatto nei rivelatori
in A e in D, si devono moltiplicare le frecce che rappresentano
i seguenti passi: un fotone va da S ad A, poi da A a D e il rive-
latore in D scatta.
Il quadrato della freccia finale dà la probabilità di questo even-
to. Essa risulta l’1% cioè la stessa di quando il foro in B è chiu-
so, perché ambedue i casi si hanno gli stessi passi.
L’altro evento completo è lo scatto dei rivelatori in B e in D.
La relativa probabilità si calcola in modo analogo e anch’essa
è circa l’1%, la stessa di quando A è chiuso.
Se si vuole sapere con che frequenza ticchetta il contatore in D
e non interessa se nel contempo è scattato A o è scattato B, la
probabilità è la semplice somma delle probabilità dei due even-
ti: il 2%.
Anche nei casi in cui si trascura qualcosa che ‘avrebbe potuto’
essere osservato per discriminare il percorso seguito dal foto-
ne, siamo di fronte a ‘stati finali’ differenti, cioè a condizioni fi-
nali distinguibili, e si devono sommare le ‘probabilità’ relative
a ciascuno di essi, non le ampiezze.
(R. Feynman, QED)